片対数グラフ

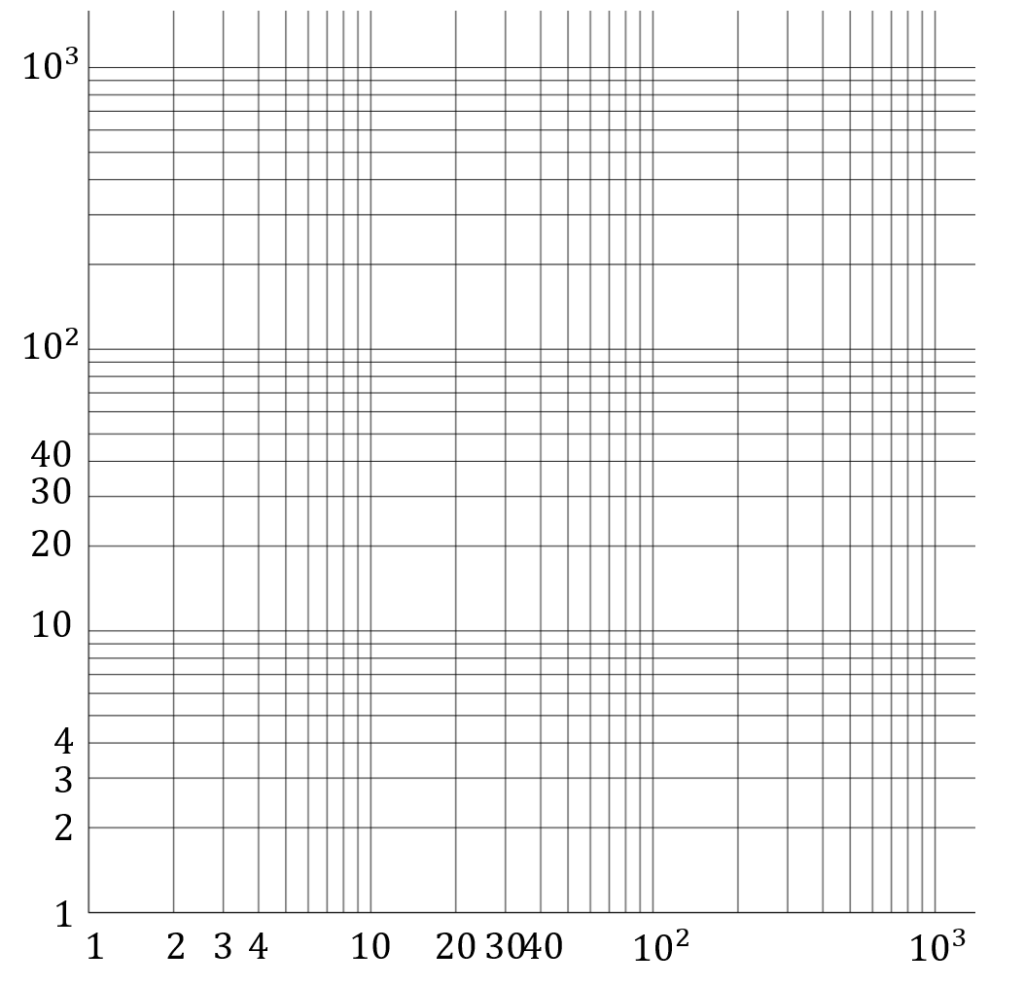
片対数グラフ（かたたいすうぐらふ、semilog graph）とは、グラフの一方の軸が対数スケール（縦を対数スケールとすることが多い）になっているグラフである。極端に範囲の広いデータを扱える。通常の目盛（線形スケール）の軸を範囲の狭いデータに、対数スケールの軸は極端に範囲の広いデータ用にする。

指数関数

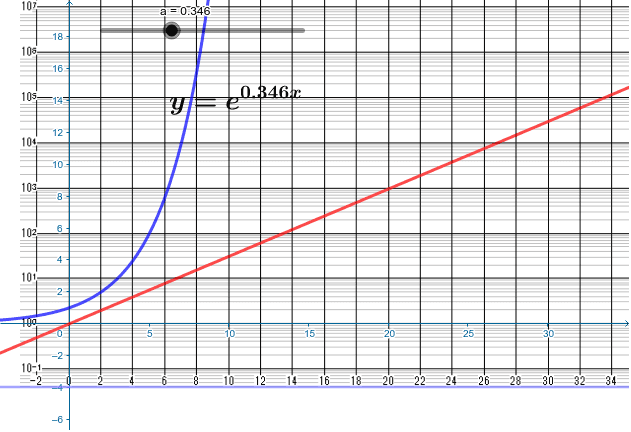
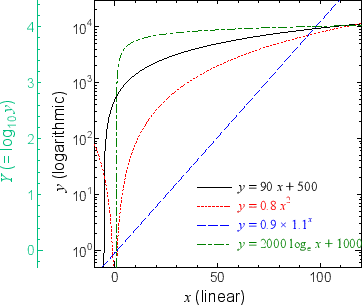
指数関数 ${\displaystyle y=a^{bx c}}$（${\displaystyle a}$ は正の定数、${\displaystyle b,c}$ は定数）の両辺の常用対数を取ると ${\displaystyle \log y=bx\log a\ c\log a}$となる。そこで横軸を通常の目盛りに、縦軸を対数目盛にすると、グラフが直線（傾き ${\displaystyle b\log a}$, y-切片 ${\displaystyle c\log a}$ の一次関数）になる。

利用例

両対数グラフ同様、乗数の値を決定するのに有効である。化学ではアレニウスプロットによって活性化エネルギーが求められる。

参考文献

関連項目

• 統計図表